Making Quad Hash-Codes for object detection and matching

05 July 2020 - 4 mins read time
Tags: Algorithms Astronomy C GSoC open-source

For matching a query image to a indexed image, it is necessary to make their hash codes from the system of 4 star objects. This layer in the detection pipeline will focus on these quad identification and their convertion to a unique hash code. The hash codes will later be stored in a KD-tree for quicks searches and retrieval with O(log(n)) time-complexity.

Table of Contents1) Quad Detection - Quads based on x-sorting - Quads based on the Nearest Neighbor Approach 2) Shift and Hash-Code formation 2.1) Angle calculation - Using vectors - Using atan2 2.2) Scale calculation 3) Conclusion

Quad Detection

This is a relatively loose but very fast heuristic which gives good results if the 2 images aren’t rotationally offset by more than 3-4 degrees. Beyond 6 degrees, the accuracy of this approach falls steeply. This is a moving window based approach in which we sort the stars within a window by their x-coordinates alone, and form quads of 4 stars sequentially from the sorted list.

We use a simple heuristic which is completely invariant to scaling and any rigid body transformation.

For each star, a quad is formed by taking the given star’s 3 nearest neighbors.

We also efficiently check if the quad isn’t duplicated each time before hashing it. Hence this is the preffered method over x-sorting. For efficient nearest neighbors queries, we first implemented a KD-Tree for stars.

Shift and Hash-Code formation

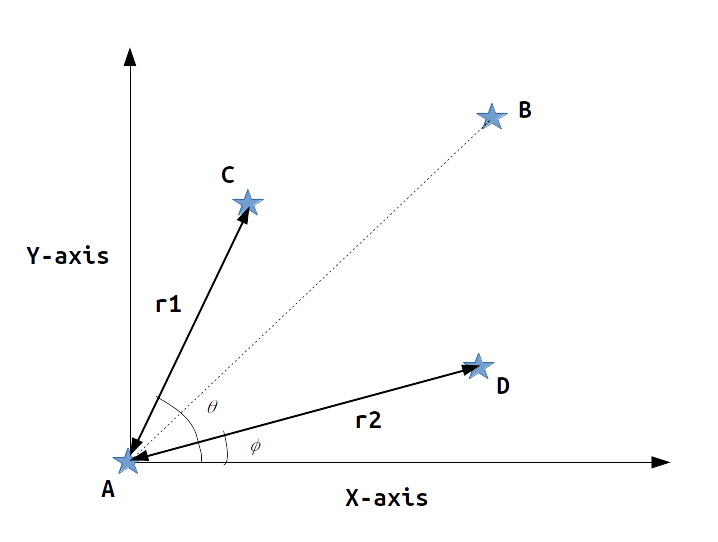
the shifted system
the shifted system

The above image shows a system of 4 stars.

Before shifting, the coordinates of any point , say, A is {A.x, A.y}. After shifting, the coordinates of point A is {0, 0} and that of B is {1, 1}. The coordinates of C and D are determined on the basis of this shift.

Angle calculation

To calculate C and D we need to know angles Ɵ and ɸ. This can be done in 2 ways:

Let AC be a vector from point A to point C and AB be a vector from point A to point B.

Now, Ɵ = arccos(AC . AB / |AC| |AB|)

And similarly for ɸ.

But this method can prove to be long and we will have to handle many cases for arccos’s domain.

A better method is to use atan2 which is provided in many programming languages, including C. It is the angle made by the vector AC with the positive X-axis.

/* atan2 */
#import <math.h>

int main(int argc, char *argv[]) {
  double theta;
  atan2(C.y-A.y, C.x-A.x);
  return 0;
}

Note: We will use original coordinates to calculate angles and later shift and use these angles for hash determination.

Scale calculation

As the points A and B are fixes now we have to determine the scale to find r1 and r2. Scale is the ratio of lengths of original AB(represented as AB.orig) and its length now.

So, scale = 1 / mag(AB.orig)

where mag(AB) is the magnitude of AB.

Therefore,

r1 = scale* (mag(AC.orig))

r2 = scale* (mag(AD.orig))

and hence,

{C.x, C.y} = {r1cos(Ɵ), r1sin(Ɵ)}

{D.x, D.y} = {r2cos(ɸ), r2sin(ɸ)}

After all this maths, lets see how the quad structure should finally look:

/* The quad structure. */
struct quad{
    double scale;
    double r1, r2;
    double theta, phi;
    double A[2], B[2], C[2], D[2];
    size_t A_id, B_id, C_id, D_id;
};

/*Hash codes. */
double hash[4] = {Cx, Cy, Dx, Dy};

Conclusion

We can use KD-tree search to make hash-codes and to filter out duplicate codes and proceed to futher layers to match these codes to the query hash-code. For angle calculation atan2 is preffered.

EOF :wave: